文／普泉精舍護法會副會長、淡江大學資訊工程學系教授　洪文斌（傳承）

「心如工畫師，能畫諸世間，五蘊悉從生，無法而不造。」

　　　　　　　　　　　　　　──《華嚴經》覺林菩薩偈

　　人工智慧（Artificial Intelligence, AI）經歷了1950年代第一波的推理期、1980年代第二波的知識期，到2010年代第三波的學習期，目前仍方興未艾，且呈爆發趨勢。由於各種軟硬體相關技術成熟，諸如平行運算速度的提升、儲存媒體容量的增大、網際網路的普及、以及機器學習演算法的長足進步，再加上巨量資料的取得容易，使得這一波AI的特點變成機器學習（Machine Learning），以大量資料為基礎，透過強大的學習演算法，自動歸納擷取其內在隱含的知識結構，進而對新的資料進行合理的預測。因此，有人說：AI學習演算法是引擎，而資料是燃料，若無燃料，再強大的引擎也無法發揮其效能。可見，處在這個AI機器學習的時代，資料的多寡決定了輸出結果的良窳。

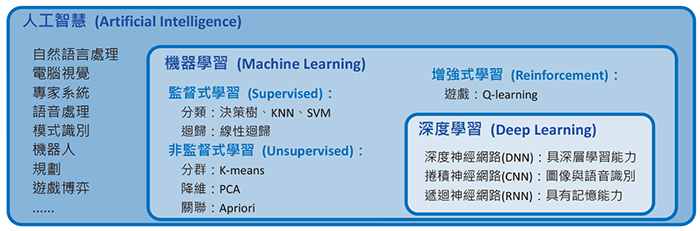圖一：AI 與機器學習和深度學習的關係

　　AI研究的範圍非常廣泛，目前最流行的機器學習只是AI的一個子領域，而深度學習（Deep Learning）又是機器學習底下的一個分支，也是目前最熱門的研究領域，其關係如圖一所示。機器學習大致可分為監督式（Supervised）、非監督式（Unsupervised）、增強式（Reinforcement）學習等三類。機器學習的應用非常廣泛，例如：垃圾郵件過濾、商品推薦、搜尋引擎、醫療診斷、視覺辨識、語音辨識、異常偵測等。而深度學習更特別擅長於視覺辨識、語音辨識、自然語言處理、生物醫學等領域。以下簡介機器學習基本常見演算法的原理，一窺AI常用的技術。

監督式學習

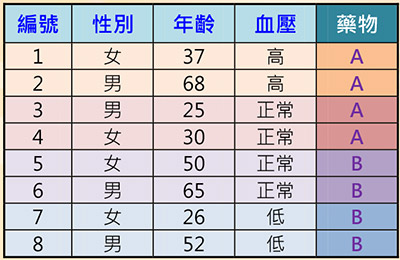表一：醫療資訊資料集範例

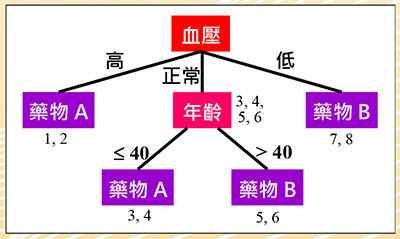圖二：醫療資訊決策樹

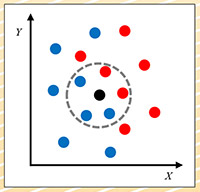圖三：K-最近鄰居法

　　監督式學習，其資料包含多個特徵（Feature）值，與其對應的標籤（Label），可能為類別或是數值；好像老師在教導學生一般，有標準答案（即標籤）。表一為一個只有八筆資料的簡單醫療資訊資料集，其性別、年齡與血壓欄位為特徵，而藥物（A或B）為標籤。透過學習演算法，訓練並建立預測模型。當有新的資料，即可使用已訓練好的模型進行預測。其主要用途有分類（Classification）與迴歸（Regression），差別在於分類的預測是類別，而迴歸的預測是數值。分類的基本演算法有決策樹（Decision Tree）、K-最近鄰居法（K-Nearest Neighbor, KNN）和支持向量機（Support Vector Machine, SVM），而迴歸則有線性迴歸（Linear Regression）。

　　決策樹：圖二為上述醫療資料集對應的決策樹，其原理即觀察每一個特徵相對於類別標籤的一致性程度，較高者則被選作分類的依據。從表一觀察得知，血壓特徵與藥物的一致性較高，因此以血壓特徵為第一個判斷的標準，依其值分為三個分支。血壓高與低分別服用藥物A和B，可以正確分類。但正常血壓的分支兩種藥物都有，我們再觀察，發現其年齡特徵與藥物的一致性較高，大於40歲服用藥物B，否則服用藥物A，完成整個分類。因此得到四條規則：
　　規則1:血壓高，服用藥物A。
　　規則2:血壓低，服用藥物B。
　　規則3:血壓正常且年齡小於或等於40歲，服用藥物A。
　　規則4:血壓正常且年齡大於40歲，服用藥物B。
此四條規則即為表一資料集的模型。假設有一筆新的資料：（女性患者，58歲，血壓正常），則可依據此模型，提供建議服用的藥物為B。

　　K-最近鄰居法（KNN）：此法不需建立模型，只需將資料集儲存起來即可。需要預測時，再計算出每一筆資料與新資料最接近的K個資料的類別，以多數決方式決定新資料的類別。圖三為KNN的一個範例，假設資料集有X和Y兩個特徵，紅與藍兩個類別，資料點分布如圖。假設K設為5，新資料以黑點表示，最鄰近的5筆資料的類別中，藍點居多，所以我們就可推論說：新資料的類別是藍色。

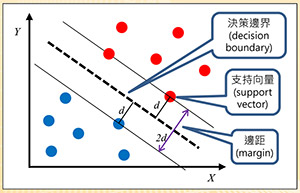圖四：支持向量機

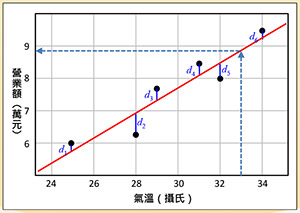圖五：線性迴歸

　　支持向量機（SVM）：圖四以簡單的兩個特徵X和Y說明SVM的原理。假設有紅藍兩個類別，其資料是線性可分割的。SVM嘗試找出一條分隔線（以虛線表示），稱為決策邊界（Decision Boundary），且與兩個類別最接近的資料點之間要等距且最大，如圖四所示。如此做的原因就是為了找到一個泛化能力（Generalization）最好的模型。此類別之間的距離稱為邊距（Margin），距離分隔線最近的點稱為支持向量（Support Vector），本法因此得名。

　　線性迴歸：例如飲料店營業額與氣溫的關係，若呈現正相關，則可用線性迴歸來預測在氣溫幾度下，營業額會是多少。圖五說明線性迴歸的原理，有六個黑色資料點，期望找到一條紅色迴歸線，使得資料點與迴歸線的距離（如圖的d1, … d6）的平方和達到最小。假設氣溫是攝氏33度，透過迴歸線，我們可以預測營業額有8.8萬元。

非監督式學習

　　非監督式學習，資料中只有特徵值，沒有標籤；如同沒有老師指導，學生自行學習。學習演算法利用資料內部隱含的結構與彼此之間的關係，嘗試找出其內在潛藏的知識。例如：透過相關性分析，將相類似的資料分成一群，稱為分群，又稱為聚類（Clustering）；透過數學轉換，保留重要訊息，而移除較不相關資訊，以降低資料儲存量，稱為降低維度（Dimensionality Reduction，簡稱降維。一筆資料若用一個欄位表達，稱為一維；若用兩個欄位表示，則為二維；若用N個欄位表達，則為N維）；或是透過頻繁樣式分析，找出資料間欄位彼此的潛在相關性，稱為關聯（Association）。分群基本的演算法有K-均值（K-means），降維則有主成分分析（Principal Component Analysis, PCA），而關聯則有Apriori演算法。

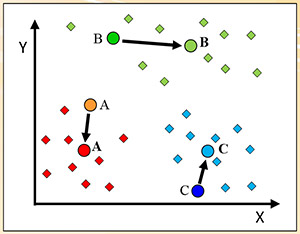圖六：K-均值法

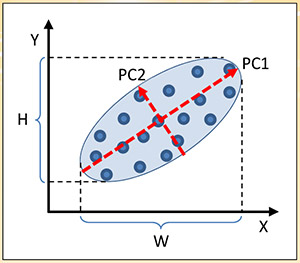圖七：主成分分析法

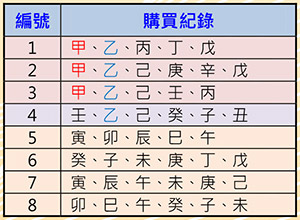表二：商品購買紀錄資料集

　　K-均值（K-means）：圖六顯示K-均值原理，假設欲將資料分為K群（此例，K=3，有紅綠藍三群），隨機選出K個資料點為各群的初始群心。然後指定每個資料點到其最近的群心的群組中，重新計算各群的新群心（以粗體字母表示）。當群心有所變動，則重新指定資料點並計算群心，直到各群的群心不變為止。此時，資料就群聚成K群了。

　　主成分分析（PCA）：圖七顯示PCA的基本原理。假設資料為X和Y二維，透過數學座標轉換，將資料分布比較廣的軸稱為PC1，分布比較窄的軸稱為PC2。可將資料點垂直投影到PC1的長軸上，其較原X軸的分布範圍W和Y軸的分布範圍H都較廣，保留更多微細的訊息。因此，可以捨棄PC2短軸的資訊，而降成一維，只剩下PC1的長軸資訊，以減少儲存空間與計算時間。

　　資料關聯性：關聯規則（Association Rule）A→B經常出現在推薦系統中，當我們購買A物品時，系統會推薦我們也可以購買B物品。表二為商品購買紀錄資料集用來說明其原理。假設有人購買了甲物，檢視紀錄，發現顧客也同時購買了乙物，因此「甲→乙」的關聯規則是否成立，取決於系統設定的信賴度（Confidence）與支持度（Support）。信賴度是指買了甲物又同時買了乙物的比例，此例為3/3=100%。支持度是指兩者同時出現在資料庫的比例，此例為3/8=37.5%。若系統設定最小信賴度為80%，最小支持度為30%，則「甲→乙」的關聯規則就成立。相反的，「乙→甲」的關聯規則就不成立，因為它的信賴度只有3/4=75%，低於系統設定的80%。

強化學習

　　強化學習，其原理是藉由定義動作、狀態與獎勵的方式，不斷訓練機器循序漸進，而學會某項任務，最常以遊戲為範例說明。例如：訓練AI玩相當流行的超級瑪莉歐（Super Mario Bros.）遊戲，設計其動作有左、右、跳三種，狀態為目前的遊戲畫面，獎勵為得分與受傷，藉由不斷訓練，而學會遊戲。常見的演算法有Q-learning。