文／普泉精舍护法会副会长、淡江大学资讯工程学系教授　洪文斌（传承）

「心如工画师，能画诸世间，五蕴悉从生，无法而不造。」

　　　　　　　　　　　　　　──《华严经》觉林菩萨偈

　　人工智慧（Artificial Intelligence, AI）经历了1950年代第一波的推理期、1980年代第二波的知识期，到2010年代第三波的学习期，目前仍方兴未艾，且呈爆发趋势。由于各种软硬体相关技术成熟，诸如平行运算速度的提升、储存媒体容量的增大、网际网路的普及、以及机器学习演算法的长足进步，再加上巨量资料的取得容易，使得这一波AI的特点变成机器学习（Machine Learning），以大量资料为基础，透过强大的学习演算法，自动归纳撷取其内在隐含的知识结构，进而对新的资料进行合理的预测。因此，有人说：AI学习演算法是引擎，而资料是燃料，若无燃料，再强大的引擎也无法发挥其效能。可见，处在这个AI机器学习的时代，资料的多寡决定了输出结果的良窳。

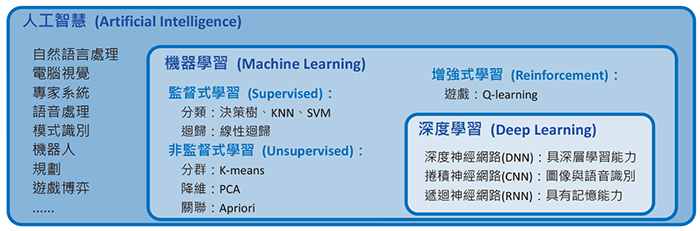图一：AI 与机器学习和深度学习的关系

　　AI研究的范围非常广泛，目前最流行的机器学习只是AI的一个子领域，而深度学习（Deep Learning）又是机器学习底下的一个分支，也是目前最热门的研究领域，其关系如图一所示。机器学习大致可分为监督式（Supervised）、非监督式（Unsupervised）、增强式（Reinforcement）学习等三类。机器学习的应用非常广泛，例如：垃圾邮件过滤、商品推荐、搜寻引擎、医疗诊断、视觉辨识、语音辨识、异常侦测等。而深度学习更特别擅长于视觉辨识、语音辨识、自然语言处理、生物医学等领域。以下简介机器学习基本常见演算法的原理，一窥AI常用的技术。

监督式学习

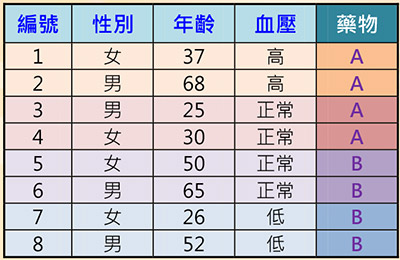表一：医疗资讯资料集范例

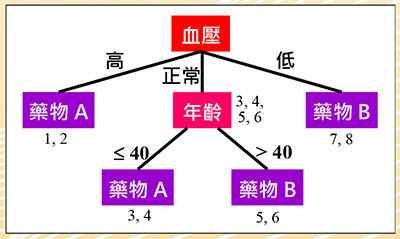图二：医疗资讯决策树

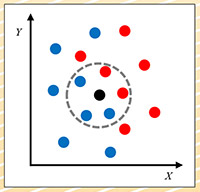图三：K-最近邻居法

　　监督式学习，其资料包含多个特征（Feature）值，与其对应的标签（Label），可能为类别或是数值；好像老师在教导学生一般，有标准答案（即标签）。表一为一个只有八笔资料的简单医疗资讯资料集，其性别、年龄与血压栏位为特征，而药物（A或B）为标签。透过学习演算法，训练并建立预测模型。当有新的资料，即可使用已训练好的模型进行预测。其主要用途有分类（Classification）与回归（Regression），差别在于分类的预测是类别，而回归的预测是数值。分类的基本演算法有决策树（Decision Tree）、K-最近邻居法（K-Nearest Neighbor, KNN）和支持向量机（Support Vector Machine, SVM），而回归则有线性回归（Linear Regression）。

　　决策树：图二为上述医疗资料集对应的决策树，其原理即观察每一个特征相对于类别标签的一致性程度，较高者则被选作分类的依据。从表一观察得知，血压特征与药物的一致性较高，因此以血压特征为第一个判断的标准，依其值分为三个分支。血压高与低分别服用药物A和B，可以正确分类。但正常血压的分支两种药物都有，我们再观察，发现其年龄特征与药物的一致性较高，大于40岁服用药物B，否则服用药物A，完成整个分类。因此得到四条规则：
　　规则1:血压高，服用药物A。
　　规则2:血压低，服用药物B。
　　规则3:血压正常且年龄小于或等于40岁，服用药物A。
　　规则4:血压正常且年龄大于40岁，服用药物B。
此四条规则即为表一资料集的模型。假设有一笔新的资料：（女性患者，58岁，血压正常），则可依据此模型，提供建议服用的药物为B。

　　K-最近邻居法（KNN）：此法不需建立模型，只需将资料集储存起来即可。需要预测时，再计算出每一笔资料与新资料最接近的K个资料的类别，以多数决方式决定新资料的类别。图三为KNN的一个范例，假设资料集有X和Y两个特征，红与蓝两个类别，资料点分布如图。假设K设为5，新资料以黑点表示，最邻近的5笔资料的类别中，蓝点居多，所以我们就可推论说：新资料的类别是蓝色。

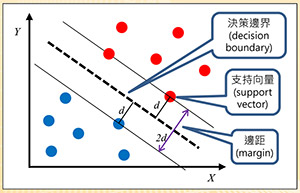图四：支持向量机

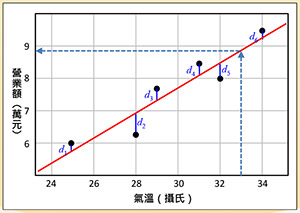图五：线性回归

　　支持向量机（SVM）：图四以简单的两个特征X和Y说明SVM的原理。假设有红蓝两个类别，其资料是线性可分割的。SVM尝试找出一条分隔线（以虚线表示），称为决策边界（Decision Boundary），且与两个类别最接近的资料点之间要等距且最大，如图四所示。如此做的原因就是为了找到一个泛化能力（Generalization）最好的模型。此类别之间的距离称为边距（Margin），距离分隔线最近的点称为支持向量（Support Vector），本法因此得名。

　　线性回归：例如饮料店营业额与气温的关系，若呈现正相关，则可用线性回归来预测在气温几度下，营业额会是多少。图五说明线性回归的原理，有六个黑色资料点，期望找到一条红色回归线，使得资料点与回归线的距离（如图的d1, … d6）的平方和达到最小。假设气温是摄氏33度，透过回归线，我们可以预测营业额有8.8万元。

非监督式学习

　　非监督式学习，资料中只有特征值，没有标签；如同没有老师指导，学生自行学习。学习演算法利用资料内部隐含的结构与彼此之间的关系，尝试找出其内在潜藏的知识。例如：透过相关性分析，将相类似的资料分成一群，称为分群，又称为聚类（Clustering）；透过数学转换，保留重要讯息，而移除较不相关资讯，以降低资料储存量，称为降低维度（Dimensionality Reduction，简称降维。一笔资料若用一个栏位表达，称为一维；若用两个栏位表示，则为二维；若用N个栏位表达，则为N维）；或是透过频繁样式分析，找出资料间栏位彼此的潜在相关性，称为关联（Association）。分群基本的演算法有K-均值（K-means），降维则有主成分分析（Principal Component Analysis, PCA），而关联则有Apriori演算法。

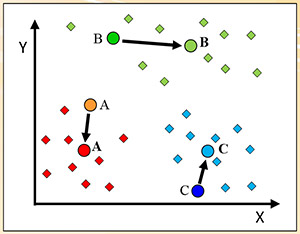图六：K-均值法

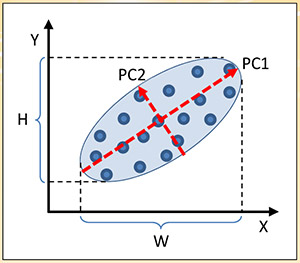图七：主成分分析法

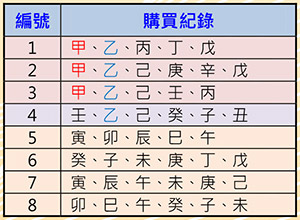表二：商品购买纪录资料集

　　K-均值（K-means）：图六显示K-均值原理，假设欲将资料分为K群（此例，K=3，有红绿蓝三群），随机选出K个资料点为各群的初始群心。然后指定每个资料点到其最近的群心的群组中，重新计算各群的新群心（以粗体字母表示）。当群心有所变动，则重新指定资料点并计算群心，直到各群的群心不变为止。此时，资料就群聚成K群了。

　　主成分分析（PCA）：图七显示PCA的基本原理。假设资料为X和Y二维，透过数学座标转换，将资料分布比较广的轴称为PC1，分布比较窄的轴称为PC2。可将资料点垂直投影到PC1的长轴上，其较原X轴的分布范围W和Y轴的分布范围H都较广，保留更多微细的讯息。因此，可以舍弃PC2短轴的资讯，而降成一维，只剩下PC1的长轴资讯，以减少储存空间与计算时间。

　　资料关联性：关联规则（Association Rule）A→B经常出现在推荐系统中，当我们购买A物品时，系统会推荐我们也可以购买B物品。表二为商品购买纪录资料集用来说明其原理。假设有人购买了甲物，检视纪录，发现顾客也同时购买了乙物，因此「甲→乙」的关联规则是否成立，取决于系统设定的信赖度（Confidence）与支持度（Support）。信赖度是指买了甲物又同时买了乙物的比例，此例为3/3=100%。支持度是指两者同时出现在资料库的比例，此例为3/8=37.5%。若系统设定最小信赖度为80%，最小支持度为30%，则「甲→乙」的关联规则就成立。相反的，「乙→甲」的关联规则就不成立，因为它的信赖度只有3/4=75%，低于系统设定的80%。

强化学习

　　强化学习，其原理是借由定义动作、状态与奖励的方式，不断训练机器循序渐进，而学会某项任务，最常以游戏为范例说明。例如：训练AI玩相当流行的超级玛莉欧（Super Mario Bros.）游戏，设计其动作有左、右、跳三种，状态为目前的游戏画面，奖励为得分与受伤，借由不断训练，而学会游戏。常见的演算法有Q-learning。